Quantum Tunnelling
Quantum tunnelling refers to the quantum mechanical phenomenon where a particle tunnels through a barrier that it classically could not surmount. This plays an essential role in several physical phenomena, such as the nuclear fusion that occurs in main sequence stars like the sun, and has important applications to modern devices such as the tunnel diode. The effect was predicted in the early 20th century and its acceptance, as a general physical phenomenon, came mid-century.

Tunnelling is often explained using the Heisenberg uncertainty principle and the wave–particle duality of matter. Purely quantum mechanical concepts are central to the phenomenon, so quantum tunnelling is one of the novel implications of quantum mechanics.
Quantum tunnelling falls under the domain of quantum mechanics: the study of what happens at the quantum scale. This process cannot be directly perceived, but much of its understanding is shaped by the macroscopic world, which classical mechanics can not adequately explain. To understand the phenomenon, particles attempting to travel between potential barriers can be compared to a ball trying to roll over a hill; quantum mechanics and classical mechanics differ in their treatment of this scenario. Classical mechanics predicts that particles that do not have enough energy to classically surmount a barrier will not be able to reach the other side. Thus, a ball without sufficient energy to surmount the hill would roll back down. Or, lacking the energy to penetrate a wall, it would bounce back (reflection) or in the extreme case, bury itself inside the wall (absorption). In quantum mechanics, these particles can, with a very small probability, tunnel to the other side, thus crossing the barrier. Here, the ball could, in a sense, borrow energy from its surroundings to tunnel through the wall or roll over the hill, paying it back by making the reflected electrons more energetic than they otherwise would have been.
The reason for this difference comes from the treatment of matter in quantum mechanics as having properties of waves and particles. One interpretation of this duality involves the Heisenberg uncertainty principle, which defines a limit on how precisely the position and the momentum of a particle can be known at the same time. This implies that there are no solutions with a probability of exactly zero (or one), though a solution may approach infinity if, for example, the calculation for its position was taken as a probability of 1, the other, i.e. its speed, would have to be infinity. Hence, the probability of a given particle’s existence on the opposite side of an intervening barrier is non-zero, and such particles will appear—with no indication of physically transiting the barrier—on the ‘other’ (a semantically difficult word in this instance) side with a frequency proportional to this probability.

The wave function of a particle summarizes everything that can be known about a physical system. Therefore, problems in quantum mechanics center around the analysis of the wave function for a system. Using mathematical formulations of quantum mechanics, such as the Schrödinger equation, the wave function can be solved. This is directly related to the probability density of the particle’s position, which describes the probability that the particle is at any given place. In the limit of large barriers, the probability of tunnelling decreases for taller and wider barriers.
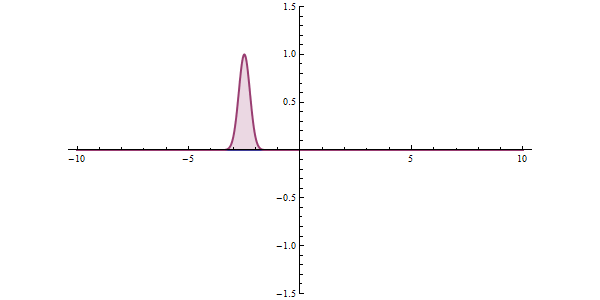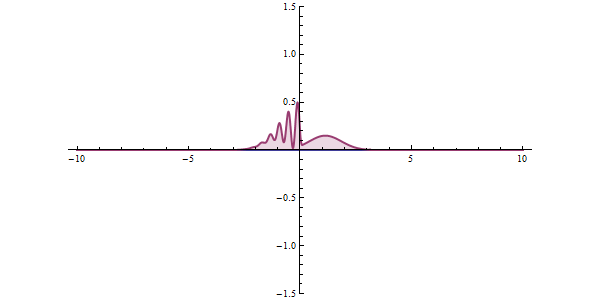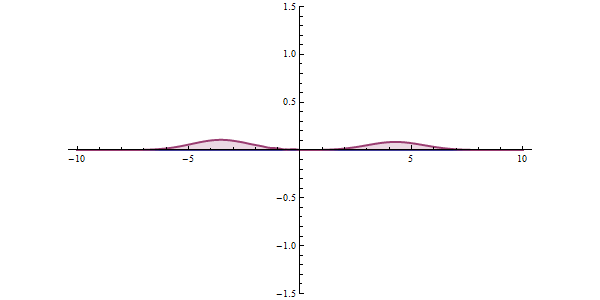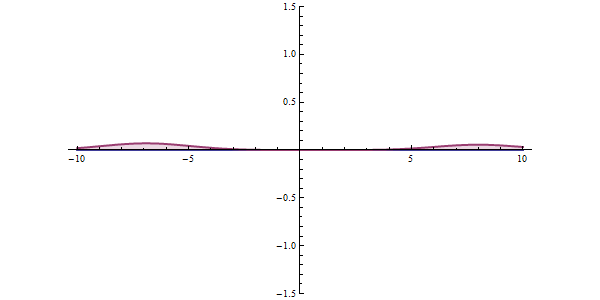
For simple tunnelling-barrier models, such as the rectangular barrier, an analytic solution exists. Problems in real life often do not have one, so “semiclassical” or “quasiclassical” methods have been developed to give approximate solutions to these problems, like the WKB approximation. Probabilities may be derived with arbitrary precision, constrained by computational resources, via Feynman’s path integral method; such precision is seldom required in engineering practice.
Related phenomena
There are several phenomena that have the same behavior as quantum tunnelling, and thus can be accurately described by tunnelling. Examples include the evanescent wave coupling (the application of Maxwell’s wave-equation to light) and the application of the non-dispersive wave-equation from acoustics applied to “waves on strings”. Evanescent wave coupling, until recently, was only called “tunnelling” in quantum mechanics; now it is used in other contexts.
These effects are modelled similarly to the rectangular potential barrier. In these cases, there is one transmission medium through which the wave propagates that is the same or nearly the same throughout, and a second medium through which the wave travels differently. This can be described as a thin region of medium B between two regions of medium A. The analysis of a rectangular barrier by means of the Schrödinger equation can be adapted to these other effects provided that the wave equation has travelling wave solutions in medium A but real exponential solutions in medium B.
In optics, medium A is a vacuum while medium B is glass. In acoustics, medium A may be a liquid or gas and medium B a solid. For both cases, medium A is a region of space where the particle’s total energy is greater than its potential energy and medium B is the potential barrier. These have an incoming wave and resultant waves in both directions. There can be more mediums and barriers, and the barriers need not be discrete; approximations are useful in this case.
See also: